Mathematik - Formeln schreiben mit TeX - Gaertner
Kursthemen
-
Mathematische Formeln in Moodle
Kathrin Gaertner, Ralf Krause
moodleSCHULE e.V.
Bertha-von-Suttner-Gesamtschule Dormagen
In diesem Kurs wird an Beispielen erklärt, wie mathematische Ausdrücke bzw. Formeln in Moodle eingebunden werden.Dazu gibt es zwei Möglichkeiten:
- Bildschirmfotos von Formeln,
die man z.B. mit dem Formeleditor einer Textverarbeitung erstellt und als Bildschirmfoto hochlädt
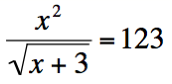
- Nutzung des TeX-Filters zur Erstellung von Formeln
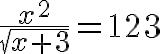
Beim Einfügen der Formeln bzw. Rechnungen als Bild entsteht der Nachteil, dass man die Ausdrücke nicht so schnell verändern kann. Man muss sie wieder neu mit einem Formeleditor erstellen, ein Bildschirmfoto machen und dieses neu hochladen. Zur Nutzung des TeX-Filters ist wichtig, dass dieser Filter vom Administrator der Moodle-Plattform eingeschaltet ist! Wenden Sie sich dafür an Ihren Administrator! - Bildschirmfotos von Formeln,
-
Befehl Beispiel Resultat \tiny $$\tiny3x$$ 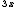
\small $$\small3x$$ 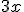
\normalsize $$\normalsize3x$$ 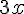
\large $$\large3x$$ 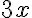
\Large $$\Large3x$$ 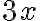
\LARGE $$\LARGE3x$$ 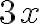
ACHTUNG:
Das Kommando für Large ist abhängig von den verwendeten Gross-/Kleinbuchstaben.
large, Large und LARGE bezeichnen verschiedene Schriftgrößen in TeX! -
-
Beachte:
Einfaches Leerzeichen (Leerschlag) und Tilden (~) werden vom TeX Filter ignoriert und produzieren gar keinen Abstand. Es muss ein definierter Formelabstand benutzt werden um ein sichtbares Ergebnis zu erzielen. -
-
-
-
Wie kann man Größe und Art der Schrift ändern?
Dafür gibt es natürlich Befehle. Für die Schriftgrößenwahl wollen
\Huge, \huge, \LARGE, \Large, \large,
eingesetzt werden, Schriftarten werden durch
\normalsize,
\small, \footnotesize, \scriptsize, \tiny\mathrm, \mathit, \mathsc, \mathbf, \mathsl, \mathsf, \mathtt
herbeizitiert. Die Kürzel seien kurz übersetzt. Der erste Befehl ist die Bezeichnung für die Normalschrift (Roman), der zweite für kursive Schrift, der dritte für SMALL CAPS, der vierte für Fettdruck, der fünfte für Slanted, der sechste für Sans Serif und der letzte für Typewriter. Jeder dieser parameterfreien Befehle wirkt solange, bis ein entsprechend anderer einen neuen Zustand herbeiführt. Soll eine Wirkung nur für einen bestimmten Bereich gelten, läßt dieses durch Einsatz einer expliziten Klammerung{und}erzielen:Normalschrift {\bf Fett} Normalschrifterzeugt: Normalschrift Fett Normalschrift.$$\mathscr{Abcde}$$
$$\mathrm{Abcde}$$
$$\mathit{Abcde}$$
$$\mathsc{Abcde}$$
$$\mathbf{Abcde}$$
$$\mathsf{Abcde}$$
$$\mathtt{Abcde}$$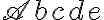
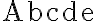
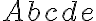
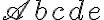
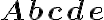
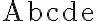
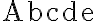
Aus: LaTeX in 7 Minuten -
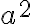
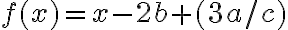
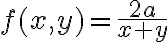
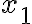
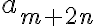
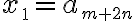
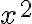
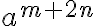
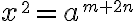
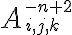
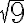
![\sqrt[n]{8} \sqrt[n]{8}](https://www.moodletreff.de/filter/tex/pix.php/31fdd78296c0c84fa011dff39e8ba0d2.gif)
![\sqrt[n]{\frac{x^n-y^n}{1+u^{2n}}} \sqrt[n]{\frac{x^n-y^n}{1+u^{2n}}}](https://www.moodletreff.de/filter/tex/pix.php/e2e1adb62f22269209aeaed8e71d40a3.gif)
![\sqrt[3]{-q+\sqrt{q^2+p^3}} \sqrt[3]{-q+\sqrt{q^2+p^3}}](https://www.moodletreff.de/filter/tex/pix.php/d33ba3b5acab8d2b62117e83ed9f7956.gif)
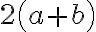
![\left[a^2+b^2\right] \left[a^2+b^2\right]](https://www.moodletreff.de/filter/tex/pix.php/8d4f94f4a962eb37286422fd9b358a81.gif)
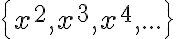
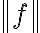
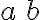
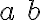
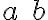


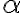
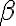
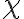
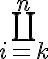
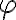
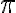
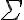
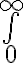
 chte gewahrt bleiben. Wahrscheinlich möchten auch Sie nicht, dass Ihre persönliche Arbeit ohne Ihr Wissen kommerziell genutzt wird.
chte gewahrt bleiben. Wahrscheinlich möchten auch Sie nicht, dass Ihre persönliche Arbeit ohne Ihr Wissen kommerziell genutzt wird.