Mathematische Formeln mit TeX
Kursthemen
-
Mathematische Formeln mit TeX
Kathrin Gaertner, Ralf Krause
Bertha-von-Suttner-Gesamtschule Dormagen
moodleSCHULE e.V.Dieser Kurs zeigt in Beispielen, wie mathematische Ausdrücke bzw. Formeln in Moodle eingebunden werden.
Dazu gibt es zwei Möglichkeiten:- Bildschirmfotos von Formeln, die mit dem Formeleditor einer Textverarbeitung erstellt und als Bild hochgeladen werden
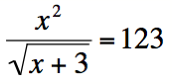
- Nutzung des TeX-Filters zur Erstellung von Formeln
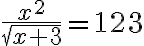
Beim Einfügen der Formeln bzw. Rechnungen als Bild entsteht der Nachteil, dass die Ausdrücke sich nicht so schnell verändern lassen. Man muss die Formeln erneut mit einem Formeleditor erstellen, ein Bildschirmfoto machen und dieses neu hochladen. Bei der Nutzung des TeX-Filters ist wichtig, dass dieser Filter vom Administrator der Moodle-Plattform eingeschaltet ist! Wenden Sie sich dafür an Ihren Administrator! - Bildschirmfotos von Formeln, die mit dem Formeleditor einer Textverarbeitung erstellt und als Bild hochgeladen werden
-
Filtereinstellungen im KursAls Trainer/in eines Kurses müssen Sie sich zuerst davon überzeugen, dass der Tex-Filter für den Ihren Kurs aktiviert ist. Öffnen Sie bitte die Filtereinstellungen in der Kurs-Administration und schalten Sie den TeX-Filter an. Falls Sie an dieser Stelle keinen Eintrag für den TeX-Filter finden. wenden Sie sich an den Administrator der Moodle-Plattform.
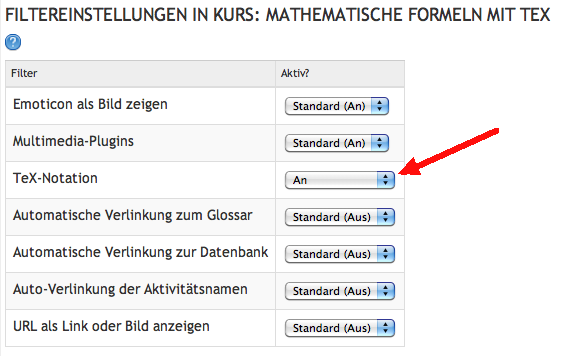
-
Mathematische Ausdrücke filtern
Der TeX-Filter gehört fest zum Lieferumfang von Moodle. Er ist dafür gedacht, TeX-Ausdrücke in Bilder (GIF oder PNG) umzuwandeln und in den Textfluss einzufügen.
Sobald der TeX-Filter aktiv ist, wandelt er mathematische Ausdrücke um, die in 2 Doppel-Dollar-Zeichen '$$ ... $$' eingeschlossen sind (hintere Spalte der Tabelle). Möchte man stattdessen, dass der Code selbst angezeigt und kein Formelbild durch den TeX-Filter erzeugt wird, so setzt man 2 Triple-Dollar-Zeichen '$$$ ... $$$' vor und hinter den Ausdruck (vordere Spalte der Tabelle).
Befehl Resultat $$ f(x)=x^2 $$ 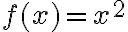
$$ f(x,y)=\sqrt{x+y} $$ 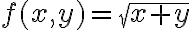
$$ f(x)=\frac{1}{2x+3} $$ 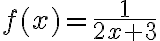
-
Arithmetische Operatoren
Arithmetische Operationen und "=" werden wie üblich eingegeben.
Befehl Resultat $$ f(x)=2x+(3a/c) $$ 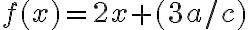
Brüche
Im eben gezeigten Ausdruck sollte der Bruch auch wirklich als solcher dargestellt werden.
Brüche sind in folgender Syntax einzugeben: \frac{numerator}{denominator}Befehl Resultat $$ f(x)=2x+\frac{3a}{c} $$ 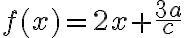
$$ f(x,y)=\frac{2a}{x+y} $$ 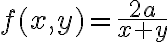
Hochgestellte Ausdrücke (Superscript oder Exponent)
Das Befehlszeichen "^" löst die hochgestellte Ausgabe der folgenden Ausdrücke aus.
Mehr als ein hochgestelltes Zeichen muss in geschweiften Klammern eingeschlossen werden { ... }.
Zur Anpassung der Schriftgröße können auch hier Größenbefehle verwendet werden!Befehl Resultat $$ x^2 $$ 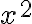
$$ a^{2m+n} $$ 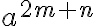
$$ x^{\small 2}=a^{\small{2m+n}} $$ 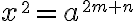
Tiefgestellte Schrift (Subscript oder Index)
Das Befehlszeichen "_" löst die tiefergestellte Ausgabe der folgenden Ausdrücke aus.
Mehr als ein tiefergestelltes Zeichen muss in geschweiften Klammern eingeschlossen werden { ... }.
Zur Anpassung der Schriftgröße können auch hier Größenbefehle verwendet werden!Befehl Resultat $$ x_1 $$ 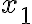
$$ a_{2m+n} $$ 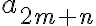
$$ x_{\small 2}=a_{\small{2m+n}} $$ 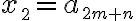
Kombination aus Superscript und Subscript
Die Ausgabe hochgestellter und tiefergestellter Zeichen lässt sich auch ganz einfach kombinieren.
Befehl Resultat $$ {\LARGE A}_{\small i,j,k}^{\small -n+2} $$ 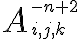
Wurzelzeichen
Wurzelzeichen können mit Exponenten und Brüchen kombiniert werden.
Wurzelzeichen können geschachtelt werden.Befehl Resultat $$ \sqrt{9}=3 $$ 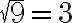
$$ \sqrt[3]{8}=2 $$ ![\sqrt[3]{8}=2 \sqrt[3]{8}=2](https://www.moodletreff.de/filter/tex/pix.php/6a529a18f1209a3f37022419459e116b.gif)
$$ \sqrt[n]{\frac{x^n-y^n}{1+u^{2n}}} $$ ![\sqrt[n]{\frac{x^n-y^n}{1+u^{2n}}} \sqrt[n]{\frac{x^n-y^n}{1+u^{2n}}}](https://www.moodletreff.de/filter/tex/pix.php/5b72b2d8e80feb92e26b64dd84f3b8d3.gif)
$$ \sqrt[3]{-q+\sqrt{q^2+p^3}} $$ ![\sqrt[3]{-q+\sqrt{q^2+p^3}} \sqrt[3]{-q+\sqrt{q^2+p^3}}](https://www.moodletreff.de/filter/tex/pix.php/e580bfddb614101dc541f896d361c8b7.gif)
-
ACHTUNG:
Das Kommando für Large ist abhängig von den verwendeten Groß-/Kleinbuchstaben. large, Large und LARGE bezeichnen verschiedene Größen! -
-
Beachte:
Einfaches Leerzeichen (Leerschlag) und Tilden (~) werden vom TeX-Filter ignoriert und produzieren keinen Abstand.
Es muss ein definierter Formelabstand benutzt werden um ein sichtbares Ergebnis zu erzielen. -
-
Array (Feld)
Syntax für einen n-dimensionalen Array: \begin{array}a1&...&an\end{array}
Befehl Resultat $$ 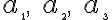 $$
$$$$ 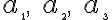 $$
$$Matrix
Eine (m,n)-Matrix wird als ein Array von m*n Elementen betrachtet, wobei jedes Element einer Spalte durch "&" und jede Zeile durch "\\" getrennt wird.
Syntax für eine (m,n)-Matrix: \begin{array}{colformat}a11&...&a1n\\a21&...&a2n\\... \\am1&...&amn \end{array}
Dabei definiert colformat das Format jeder der n Spalten: l für links, r für rechts und c für zentriert.
Mit der Anweisung {ccccc} könnte eine (m,5)-Matrix formatiert werden, in der alle Spalten zentriert ausgerichtet sind.
Im Beispiel wird die Anweisung {lcr} für die Matrix verwendet, um Spalte 1 links, Spalte 2 zentriert und Spalte 3 rechts auszurichten.Befehl Resultat $$ \left(\begin{array}{lcr}a_{\tiny1}+d & a_{\tiny2}+d & a_{\tiny3}+d \\ b_{\tiny1}& b_{\tiny2}& b_{\tiny3} \\ c_{\tiny1} & c_{\tiny2} & c_{\tiny3} \end{array}\right) $$ 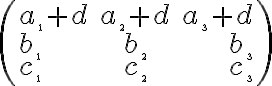
-
-
-
-
-
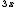
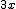
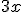
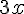
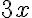
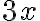
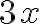
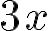
![\left[a^2+b^3\right] \left[a^2+b^3\right]](https://www.moodletreff.de/filter/tex/pix.php/edf04be7a6ecdd2ff7aea05053dbf5ae.gif)



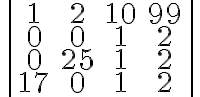
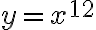
 gewahrt bleiben. Wahrscheinlich möchten auch Sie nicht, dass Ihre persönliche Arbeit ohne Ihr Wissen kommerziell genutzt wird.
gewahrt bleiben. Wahrscheinlich möchten auch Sie nicht, dass Ihre persönliche Arbeit ohne Ihr Wissen kommerziell genutzt wird.